Introduction to Computer System 計算機概論: 3月 2012

第02章數字系統與資料表示法

2-4數值算數運算

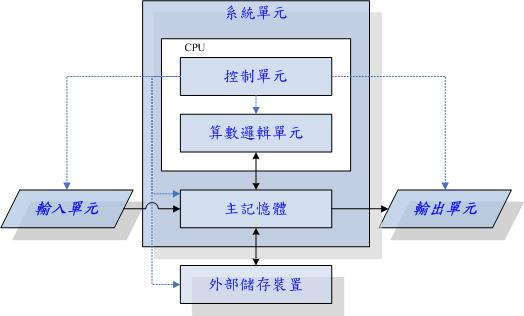
無號整數乘法的硬體方塊圖

無號整數乘法之流程圖

無號整數乘法

二進位乘法計算

兩個基底相同的數欲做乘法運算時應先將欲相乘的數值轉換成十進位再做相乘計算，而計算結果則需再化成原基底值

2-6浮點數表示法

浮點數（float)：

是屬於有理數中某特定子集的數的數字表示，在計算機中用以近似表示任意某個實數。具體來說，這個實數由一個整數或定點數（即尾數）乘以某個基數（計算機中通常是2）的整數次冪得到，這種表示方法類似於基數為10的科學記數法。

浮點計算是指浮點數參與的運算，這種運算通常伴隨著因為無法精確表示而進行的近似或舍入。

一個浮點數a由兩個數m和e來表示：a = m × b^e。在任意一個這樣的系統中，我們選擇一個基數b（記數系統的基）和精度p（即使用多少位來存儲）。m（即尾數）是形如±d.ddd...ddd的p位數（每一位是一個介於0到b-1之間的整數，包括0和b-1）。如果m的第一位是非0整數，m稱作正規化的。有一些描述使用一個單獨的符號位（s 代表+或者-）來表示正負，這樣m必須是正的。e是指數。

這種設計可以在某個固定長度的存儲空間內表示定點數,但無法表示的更大範圍的數。

例如，一個指數範圍為±4的4位十進制浮點數可以用來表示43210，4.321或0.0004321，但是沒有足夠的精度來表示432.123和43212.3（必須近似為432.1和43210）。當然，實際使用的位數通常遠大於4。

此外，浮點數表示法通常還包括一些特別的數值：+∞和−∞（正負無窮大）以及NaN（'Not a Number'）。無窮大用於數太大而無法表示的時候，NaN則指示非法操作或者無法定義的結果。

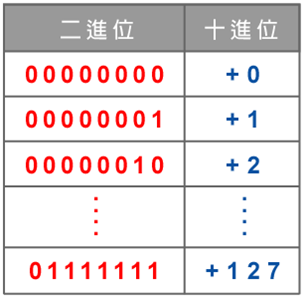
•符號位元(1位元)代表±
—0為正、1為負

•有效數(23位元)代表小數點後的數字(也稱假數)

—小數點前的數字總是1

•偏移指數(8位元)代表必須減127的指數

—指數會指出小數點真正的位置

• 因此浮點表示法為±(1.有效數) x 2偏移指數-127

單精密度浮點表示法：

下面是MIPS浮點數字的表示法， S 是浮點數字的正負符號（1表示負號），指數放在8位元指數欄位（包括指數的正負符號），有效數字是23位元的小數，這種表示法稱為 sign and magnitude表示法。

倍精密度浮點表示法

倍精密度浮點數字的表示法需要兩個字組，如下圖所示，S是數字的正負位元，指數放在11個位元的指數欄位，有效數字是52位元的小數。

2-11誤差與錯誤檢查

錯誤更正碼 (ECC)

ECC英文全名為Error Checking and Correction Code，中文名稱為錯誤修正碼檢查。

ECC是使用一種特殊電路，利用較複雜的演算法檢查儲存在記憶體中的資料是否一致。ECC通常在每個byte的資料使用3bit來作檢查碼。而且它不只是可以從多個位元中找出其中錯誤，並且可以將錯誤的位元並予以更正。一個有ECC的系統，不僅能容許錯誤，並可以將錯誤更正，使系統得以持續正常操作，不致因錯誤而中斷。ECC稱為「錯誤自動檢查與更正」，這也是一種資料檢查的技術，可以檢查資料是否正確；和Parity Check主要的不同點是在只有一個錯誤的狀況下，ECC具有自動更正的能力。

記憶體要具有檢查與修復的功能，就必須記錄更多的資訊，因此這類的記憶體除了負責資料的記錄之外，還要更多的記憶體來保存核對與更正所需的資訊。以前述的Parity Check為例，每8個位元需要增加1個位元來處理。ECC也是類似的做法，但每家廠商的做法並不完全相同，必須視處理資料的方式而定，例如Intel以64個資料位元搭配8個ECC位元，另外也有以8個資料位元搭配4個ECC位元的做法。

到目前為止ECC大約分為三個支流兩種形式

1.代數碼:
Hamming-code RS-code BCH-code RM-code等等都能歸類為這種碼，這種碼的特徵是需要相當嚴謹的代數理論(finite field)，其解碼方法也都是一種編碼對映一種解碼

2.幾何碼:
這種碼已經式微除了少數的數學家外根本沒人在討論，因為其數學理論太過艱深需要扯到代數幾何的概念，再ECC聖經本上有提到一種接近幾何碼的code:EG-code跟PG-CODE

3.圖論碼:
目前ECC學界最新的一種討論碼的方式，這種碼是利用圖學中factor-graph以及sum-product的概念來從事編碼及解碼其特徵是概念簡單，只需掌握住factor-graph的基本特性跟sum-product的演算規則

漢明碼

編碼後數據位置		p1	p2	d1	p4	d2	d3	d4	p8	d5	d6	d7	d8	d9	d10	d11	p16	d12	d13	d14	d15
數據位位置		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	...
奇偶校驗位覆蓋率	p1	X		X		X		X		X		X		X		X		X		X
	p2		X	X			X	X			X	X			X	X			X	X
	p4				X	X	X	X					X	X	X	X					X
	p8								X	X	X	X	X	X	X	X
	p16																X	X	X	X	X

在邏輯學中，邏輯算符異或（符號為XOR或EOR或⊕）是對兩個運算元的一種邏輯析取類型。但與一般的邏輯或不同，異或算符的值為真僅當兩個運算元中恰有一個的值為真，而另外一個的值為非真。轉化為命題，就是：「兩者的值不同。」或「有且僅有一個為真。」

兩個運算元（命題）：A與B的異或一般寫成A異或B，或者寫成 $A XOR B$ 、 $A \oplus B$ 、 $A \neq B$ 等等。在C語言中，寫作A^B。

$A \oplus B$

第02章數字系統與資料表示法

2-3整數表示法

一個位元(Bit)可代表 0 或 1 兩種狀態，我們取其最高位元來代表正負數，以0代表正數，而以1代表負數

以一個位元組來講，若它所儲存的資料並沒有負數(例如庫存的庫存量、單價)，那8個位元可代表256 (28=256) 種狀況，它的數字範圍可為0~255。

電腦最基本的運算方式為加法。因電腦上為了簡化減法與除法的電路設計，因此，遂採用補數的方法來表示負數。利用加法，加其負數(用2的補數表示法代替)，即得減法功效。若利用8 bit來表達整數型態資料，且最左位元0代表正數，1代表負數，負數與正數間互為2的補數，則可表示之範圍為 -128～+127，即-2^n-1～+2^n-1。

補數(Complement)： 是指兩個數字加起來等於某數時，則稱該二數互為某數的補數；例如3的10補數為7，同理7的10補數為3。而補數有助減法運算用加法器來執行。例如4的十進位補數為6，故：

算術溢位（arithmetic overflow）或簡稱為溢位（overflow）指的是：
1. 在電腦領域裡所發生的溢位條件是，執行單項數值計算時，當計算產生出來的結果是非常大的，大於暫存器或記憶體所能儲存或表示的能力限制。
2. 在電腦領域裡，執行多項或累計的數值計算時，當計算產生出來的總值是非常大的，大於暫存器或記憶體所能儲存或表示的能力限制。要注意的是，溢位可能會在其他位址被置換
1的補數系統(1's Complement)：

1補數系統是指兩數之和為1，則此兩數互為1的補數，亦即0和1互為１的補數。換言之，
欲求得二進位數的1補數，只需將0變成1，1變成0即可；例如1010 的1補數為0101。